The Biology Researcher's Guide to Choosing Correct Statistical Tests
Picking the correct statistical test is as important as your experimental technique.
Meanwhile, many researchers rush to do t-tests! This mistake yields a lot of false positives or missed discoveries.
In this article, Wildtype One combined everything a biologist needs to choose the correct test in GraphPad Prism, get accurate analyses, and have reproducible results.
Let's start.
We will walk you through (Table of Content):
I. 5 Common Statistical Mistakes in Biology Labs
II. Paired vs. Unpaired Data
III. Choosing the Right Test
IV. Don’t do t-tests after ANOVA
V. Survival Analysis and Log-rank Tests
VI. Case Studies & Practical Examples
VII. Software-Specific Tips for GraphPad Prism Users
VIII. Final Thought
🧫 Join our network of 400+ elite researchers by signing up for Wildtype One’s FREE newsletter.
I. 5 Common Statistical Mistakes in Biology Labs
Picking the wrong test happens frequently in labs, and can lead to false positives or missed discoveries.
For example, choosing the wrong assumptions when comparing Western blot protein bands, your experiment’s reproducibility suffers.
Similarly, survival data are usually non-normal and censored, so they require special methods (Kaplan–Meier curves and log-rank tests) instead of a simple mean comparison.
A few statistical mistakes happen often in laboratories. Here’s a list:
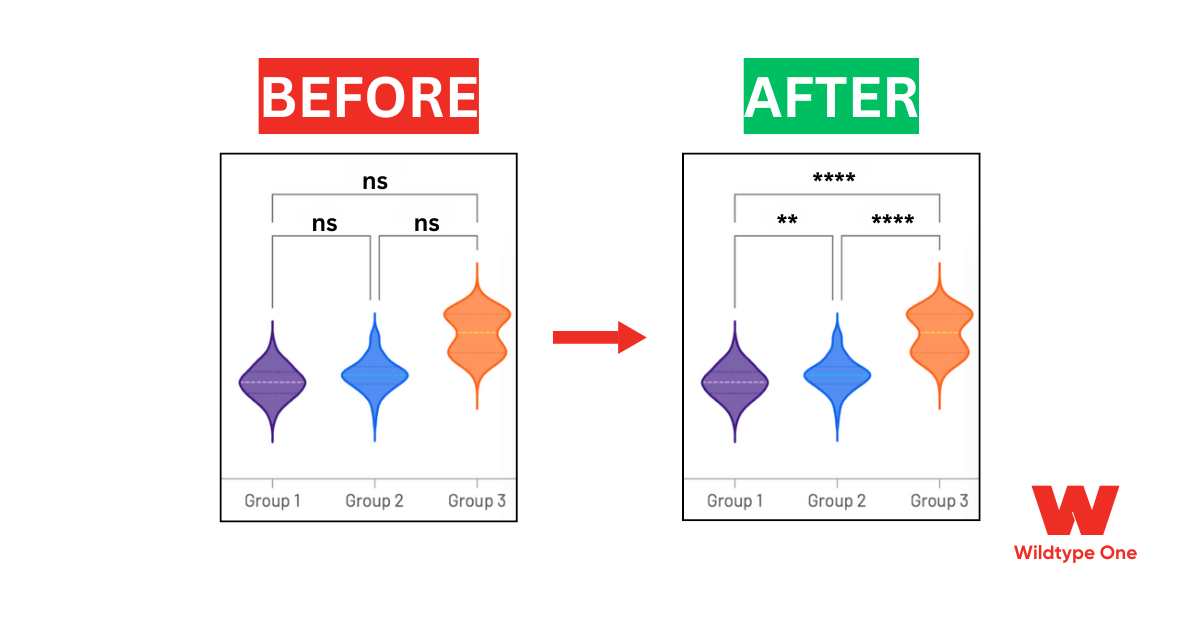
Mistake #1 - Multiple t-tests instead of ANOVA (p-hacking)
Remember the infamous example where researchers found “significant” brain activity in a dead salmon because they didn’t correct for multiple comparisons?
More tests = higher false positive chance.
Performing many separate t-tests on multiple groups or time points without adjustment is a mistake.
This is called “p-hacking” and can yield significant p-values by pure chance.
To do: Choose a test that considers all groups at once (e.g., ANOVA for >2 groups) or use proper multiple comparison corrections.
Mistake #2 - Misunderstanding p-values
p>0.05 doesn’t always mean “no effect.” It could also mean insufficient data/power.
Conversely, p<0.05 doesn’t prove scientifically meaningful or reproducible results. Focus on effect sizes and confidence intervals, and be cautious not to “chase” arbitrary significance thresholds.
To do: As a rule, never assume a lack of significance proves two conditions are the same ref – it might just mean you need a larger sample.
Mistake #3 - Ignoring assumptions
The mistake here is twofold:
Parametric tests (t-test, ordinary ANOVA) on data that are NOT normally distributed or have unequal variances
Automatically using a non-parametric test (Mann–Whitney or Kruskal–Wallis) without considering its drawbacks.
Statistical tests have assumptions (normality of data, equal variances, independent samples, etc.).
Non-parametric tests don’t assume normal data, but they generally have less power and can test medians rather than means.
To do: Always examine your data (e.g., with Prism’s normality tests or a QQ plot). Also consider sample size and whether violations are severe.
Mistake #4 - Improper pairing or independence
If you have measurements that are naturally paired (e.g., before/after from the same subject, or controls and treated samples run in parallel), using an unpaired test wastes statistical power.
Conversely, treating independent samples as paired will also give wrong results.
To do:
Use unpaired tests for For “test vs. control” type of sample
Use paired tests when the measurements are on the same subject over time or on two different subjects handled together (seeded from the same cell line for example).
Mistake #5 - No correction for multiple comparisons
If you compare many groups or endpoints (common in omics studies or multi-endpoint experiments), you must correct for multiple comparisons. Failing to do so means a higher chance that any “significant” difference is a false alarm.
To do:
Prism offers built-in corrections (Bonferroni, Holm-Šidák, false discovery rate, etc.) – use them!
E.g., if you test hundreds of genes or perform numerous post-hoc tests, control the False Discovery Rate (FDR) rather than just reporting raw p-values.
Now let’s look at important statistical notions scientists should know.
II. Paired vs. Unpaired Data
One of the first decisions is whether to use an unpaired or paired test. This depends on your experimental design:
Unpaired
The two groups you’re comparing are independent.
Example 1: Comparing protein expression in treated vs. control cells.
Example 2: Comparing tumor sizes in mice Group A vs. Group B.
Each sample is separate. Different subjects.
An unpaired t-test (for two groups) or ordinary one-way ANOVA (for multiple groups) is appropriate if each data point is from a different, unrelated subject.
Paired
Measurements come from the same subject under different conditions.
Classic example: Measuring heart rate in the same person before vs. after drinking coffee.
Example 2: In biology, this is equivalent to monitoring the same cell line growth or tumor volume before and after drug treatment (repeated measures experiment)
In these cases, each subject or matched pair serves as its own control. Each has its own variability. A paired test gives you more statistical power.
Important distinction: If your two conditions (treated vs. control) were run together in parallel (e.g. coming from the same batch of cells) they should also be paired!
How to tell in Prism?
When you choose a t-test or ANOVA in GraphPad Prism, it will ask if your data are “paired or unpaired.”
Choose “paired” if each row of your data table represents a matched set of observations (e.g., pre vs post for each patient, or a block of experiments run together).
By contrast, select “unpaired” if your groups are independent (different animals or samples).
III. Choosing the Right Test
Now let’s walk through how to select an appropriate statistical test in Prism step by step.
Type of data
Number of groups
Distribution assumptions
Whether your design is paired
Here’s a decision guide below:
Parametric or Non-Parametric?
First, determine if your data meet the assumptions for parametric tests.
With large sample sizes, mild deviations from normality are usually OK. But with small n (common in biology), a few outliers or a skewed distribution can violate assumptions.
Parametric tests compare means and generally have more power when assumptions are met. Non-parametric tests compare ranks or medians and make fewer assumptions, at the cost of some power.
If your data are roughly bell-shaped (normal distribution; symmetrical; no dramatic variations or many outliers) and measured on an interval/ratio scale, parametric tests are preferred because they make full use of the data. E.g., tumor weights, gene expression levels (after log-transform), or cell viability percentages often use parametric tests if sample size is decent.
If your data are ordinal or very skewed (maybe some tumors shrunk dramatically, while others didn't), or your sample size is small and suspect normality is way off, use a non-parametric test.What are the tests?
What are the tests?
Parametric tests
For parametric, two-group comparisons, use the t-test (paired on unpaired)
For >2 groups, use ANOVA
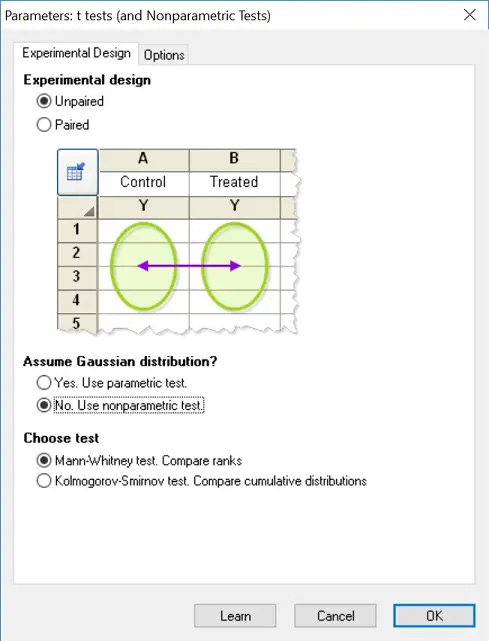
Non-parametric tests
For two-group comparisons, the Wilcoxon matched-pair test (paired) or the Mann–Whitney U test (unpaired) are the non-parametric alternative to the t-test
For >2 groups, Kruskal–Wallis is the alternative to one-way ANOVA.
How to tell in Prism?
GraphPad Prism can perform both types. If you select a t-test in Prism and then choose “non-parametric”, it will usually adjust automatically (e.g., “Mann-Whitney” instead of “t-test”).
Prism also notes that non-parametric tests focus on medians. E.g., the Mann–Whitney test determines if there’s a difference in medians between two groups (assuming the distributions have the same shape). Likewise, the Kruskal–Wallis test checks if at least one group’s median is different among multiple groups.
Use these when medians (or rank orders) are more reliable than means (for instance, when a few extreme values would distort the mean).
Just be aware that if sample sizes are tiny, non-parametric tests have very little power to detect differences. In some cases, a data transformation (like log or square-root) can normalize data enough to use a parametric test with greater power.
Tip: Don’t automate the choice purely via a normality test. GraphPad’s advice is clear: “Normality tests should not be used to automatically decide whether or not to use a nonparametric test”. Instead, consider the shape of the distribution and the scientific context. If in doubt, you can run both a t-test and a Mann-Whitney to see if they agree – just don’t report the one that “looks better” without justification (that’s p-hacking!). Decide on your approach a priori whenever possible.
Important exception
If you have categorical outcomes (yes/no, success/failure) instead of continuous data for two groups, you wouldn’t use a t-test at all – you’d use a Chi-square or Fisher’s exact test. Prism can do those as well, but our focus here is measurement data.
IV. Don’t do t-tests after ANOVA
Let’s say your ANOVA (or Kruskal–Wallis) compares several groups and finds a difference. This means at least one of the groups is different from the others. The next question is “which groups differ?”.
A common mistake here is doing manual t-tests between groups to know which one is different. This is prone to too much error.
Instead, you will do a post hoc test. This is where you go ninja mode in statistics.
Post hoc tests are essentially pairwise comparisons between groups, done in a way that controls the overall error rate.
GraphPad Prism makes post hoc testing easy: in the ANOVA dialog, there’s a “Multiple Comparisons” tab where you can choose the test for pairwise comparisons.
Here are some guidelines:
1. Tukey’s HSD test – Use this when you want to compare every group with every other group (all pairwise comparisons). Tukey’s is a popular choice because it rigorously controls the family-wise error rate and is designed for equal sample sizes (but is fine with slight inequalities). Prism recommends Tukey for all-pairs comparisons. For example, if you have 4 groups and want to know which specific pairs are significantly different, Tukey’s test will give you adjusted p-values for each of the 6 pairwise comparisons. It’s a good all-purpose choice. In Prism, just select “Tukey” in the multiple comparisons dropdown for one-way ANOVA.
2. Bonferroni (or Šidák) correction – Bonferroni is quite conservative, it simply multiplies each p by the number of comparisons. Šidák is similar but slightly less conservative for many comparisons. These can be useful if you have a small number of planned comparisons rather than all pairs. Prism might list “Bonferroni” results if you choose that option. With many groups, Tukey’s and Bonferroni often give similar conclusions; Tukey is more optimized for all-pairs, while Bonferroni is generic.
3. Dunnett’s test – Use Dunnett’s when you only compare each treatment group against a single control, not every pair. Dunnett’s test controls the error rate for multiple comparisons to a control and is more powerful than Tukey in that scenario. In Prism’s options, choose “compare every mean to control” and select Dunnett. Prism will then ask which group is the control. Dunnett’s is great for dose-response or variant-vs-wildtype comparisons where the baseline control is the reference.
4. Holm-Šidák or Holm-Bonferroni – Holm’s step-down methods (Holm-Šidák) are a bit more powerful than straight Bonferroni while still controlling family-wise error. These are good default choices if you have a custom set of comparisons or want a generally robust correction. If you select “Explore all comparisons” = No in Prism and then specify a handful of pairs, Prism might use the Holm method by default. Holm’s method is uniformly as good or better than Bonferroni's.
5. Dunn’s test (for Kruskal–Wallis) – If you ran a Kruskal–Wallis (non-parametric ANOVA) and found a significant difference, you can do multiple comparisons on ranks as well. Prism will use Dunn’s test for non-parametric post hoc comparisons. Note: By default, Prism’s Dunn can be without correction (which is anticonservative) or you can apply Bonferroni to the Dunn p-values. Prism’s guide mentions that for nonparametric, it doesn’t automatically correct unless you specify (so be careful to choose the corrected option).
6. False Discovery Rate (FDR) – If you have many comparisons—like dozens or more (e.g., gene expression changes across conditions, or a large number of endpoints), controlling the FDR is often more appropriate than strict family-wise corrections. Prism offers FDR methods (Benjamini–Hochberg and two variants) in the multiple comparisons dialog. You can choose a Q value (e.g., 0.05) which is the acceptable false discovery rate. This is very useful for high-throughput data or ‘omics where you expect some proportion of false hits and want to limit that proportion. Prism will label comparisons as “discoveries” if they meet the criterion.
Important note:
In all cases, make sure you report which post hoc test you used. It’s not enough to say
“ANOVA was significant, p<0.01”
–readers will want to know which groups differed.
Instead, you might report:
“One-way ANOVA showed a significant effect of treatment (p<0.001). Post hoc Tukey’s test indicated that high-dose treated cells had higher apoptosis than control (p=0.002), whereas low-dose was not different from control (p=0.45).”
Prism’s output will provide these pairwise p-values for you. It may also give confidence intervals for differences. Be mindful of confidence intervals crossing zero – if they do, that difference is not significant (Prism usually flags this with “ns”).
V. Survival Analysis and Log-rank Tests
This is a special kind of data that requires its own analysis, so we gave it its own section.
Survival data (time-to-event data) is common in cancer research – e.g., time to death, disease-free survival, or progression-free survival. These require different methods because of:
censoring (when subjects haven’t had the event by the end of the study or are lost to follow-up), and
non-normal distribution of times. Instead of means, we compare survival curves.
The go-to method is the Kaplan–Meier estimator to plot survival curves, and the log-rank test to compare them.
GraphPad Prism has a dedicated survival analysis section for this.
Here’s how to proceed:
Kaplan–Meier Curves: In Prism, you’d create a “Survival” data table, entering the survival time for each subject and an indicator if the event (e.g. death) occurred or the data is censored at that time. Prism will then plot a stepwise Kaplan–Meier curve for each group. This curve shows the probability of remaining event-free over time. It accounts for censored subjects (often plotting a small tick mark for a censored observation). You can visually compare curves for, say, a treatment vs control group, or different patient subgroups. The median survival for each group can be read from the plot (the time at which survival probability = 0.5).
Log-rank test: To statistically compare two (or more) survival curves, use the log-rank test (also called the Mantel–Cox test). This test checks the null hypothesis that there is no difference in survival between the groups across time. It is a non-parametric test that essentially compares the observed vs. expected number of events in each group at each time point, summing across the follow-up. In Prism, after entering survival data, choose Analyze → Survival (Kaplan–Meier) → Compare survival curves. Prism will output a p-value for the log-rank test (and often a hazard ratio if two groups). For example, you might see “Log-rank test p = 0.003” comparing survival curves. This indicates a significant difference in the overall survival distribution between groups.
Note:
The log-rank test does not tell you where the curves differ or by how much, just that they are significantly different overall. Also, it gives equal weight to all time periods (which is usually fine; if you needed to adjust for covariates or weight early vs late differences, that’s where Cox regression comes in – more advanced).
Now, let's look at practical, everyday examples from a biology lab and how to deal with them.
🧫 Join our network of 400+ elite researchers by signing up for Wildtype One’s FREE newsletter.
VI. Case Studies & Practical Examples
Let’s apply these principles to some real-world examples relevant to cancer and cell biology research:
Example 1: Western Blot Quantification
Quantifying Western blots requires statistical analysis. (Photo credit: Bell G. BMC Biol. 2016)
Scenario
You ran Western blots to compare a protein’s expression between untreated control cells and drug-treated cells. You have densitometry values from 3 independent experiments (each with a control and treated sample).
How to analyze?
Correct analysis
Each experiment’s control and treated are paired (run and measured together), so you could use a paired t-test comparing treated vs control. Pairing makes sense because experiment-to-experiment variability in blot exposure or loading will affect both control and treated similarly.
By pairing, you essentially ask: “on each experiment day, did treatment increase the protein compared to control?” This controls for day-to-day variability.
In Prism, you’d enter the 3 pairs of values and choose a paired t-test. If the data were very skewed or non-normal (perhaps Western blot data often are percentages or ratios), you might instead do a Wilcoxon matched-pairs test.
If the design was unpaired – say you had 5 control cell cultures and 5 treated, all handled separately – then an unpaired t-test would be used.
Always ensure you had sufficient replicates (technical repeats don’t count as independent replicates).
If you have more than two groups (e.g., control, low dose, high dose on the same blot), use one-way ANOVA with repeated measures if each blot contains all conditions. Western blots often have small sample sizes, so it’s extra important to avoid over-interpretation of a borderline p-value.
To avoid bias, plan your stats before running our gel (how many blots, how you’ll quantify and compare).
Example 2: Drug Treatment Dose Response
Dose-Reponse analysis cannot be performed using a regular t-test. (Photo credit: TMedWeb)
Scenario
You’re testing the effect of a cancer drug on cell proliferation. You treat cells with 0 (control), 1 μM, 10 μM, or 50 μM of the drug, with 5 independent cell culture replicates per group. After 72 hours, you measure an optical density (OD) as a proxy for cell number.
How to analyze differences across doses?
Correct analysis
This calls for a one-way ANOVA (since 4 groups) followed by post hoc tests.
In Prism, you’d enter the OD values under columns labeled 0, 1, 10, 50 (μM). First, check if variances look comparable and the data roughly normal (OD measurements often are fairly normal if the range isn’t huge). Run One-way ANOVA. If p < 0.05, it indicates the drug concentration has a significant effect on cell proliferation.
To find out where, use a post hoc test:
Since you likely want to compare each dose to the control, Dunnett’s test is ideal. Prism can perform Dunnett’s, giving you (for example) p=0.8 for 1 μM vs 0 (no sig. difference), p=0.02 for 10 μM vs 0 (significant reduction), and p<0.001 for 50 μM vs 0 (highly significant). This tells a clear story: only the higher doses significantly inhibit proliferation compared to control.
If you also cared about differences between the doses themselves (not just vs control), you might choose Tukey’s test instead, which would compare all pairs (e.g., showing 50 μM is also different from 1 μM, etc.).
Since dose is a continuous factor, another approach is to test for a trend – Prism has a test for linear trend in one-way ANOVA. That can tell you if there’s a significant dose-response trend across increasing concentrations. In our case, we might expect a linear or saturating trend with higher doses giving lower OD.
You could report:
“One-way ANOVA showed a significant effect of drug dose on cell proliferation (F(3,16)=15.2, p<0.0001). Dunnett’s post hoc test revealed that 10 μM and 50 μM doses had significantly lower OD than control (p<0.05 and p<0.001, respectively), while 1 μM had no significant effect (p>0.05).”
This communicates the findings with appropriate stats.
Parametric ANOVA is usually robust for moderate deviations, especially with equal n. But if data were not normal (skewed), switch to Kruskal–Wallis and Dunn’s test.
Example 3: Survival Analysis of Treated vs Untreated Mice
Mice survival analysis is a classic case of the log-rank test. (Photo credit: Laura Ferrer Font via ResearchGate)
Scenario
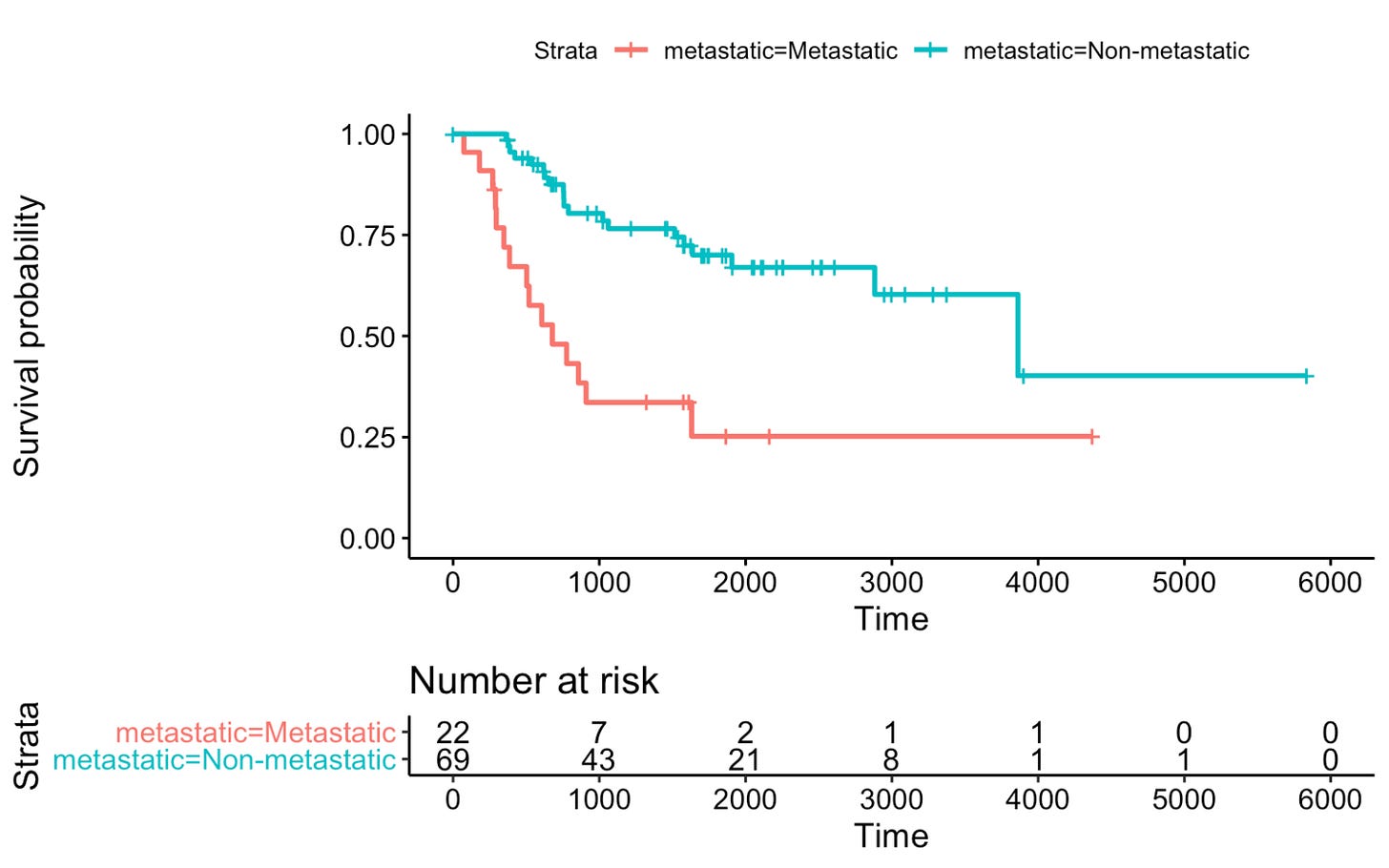
You have a mouse study with two groups: one group of tumor-bearing mice gets a new therapy, another group is a control with no treatment. You follow them for 12 months to see when they die (survival time). At the end, you draw Kaplan–Meier curves for the two groups.
How to compare survival?
Correct analysis
This is a classic case for the log-rank test.
In Prism, input each mouse’s survival time and an event indicator (1=dead, 0=censored if alive at study end).
Suppose many mice survive longer in the treated group, while they most die earlier in the control group. The Kaplan–Meier curves will separate, with the treated curve lying above the control curve.
To see if this difference is significant, you run “Compare survival curves (log-rank test)” in Prism.
Prism reports Log-rank (Mantel-Cox) chi-square = 5.4, p = 0.020 for example.
This means there is a statistically significant difference in survival between the two groups.
You would report:
“Mice receiving the therapy had prolonged survival compared to controls (median 300 days vs 210 days). Kaplan–Meier analysis with a log-rank test showed a significant improvement in survival (p=0.02) in the treated group.”
This informs readers that the entire survival curve differed.
You might also note median survival times. E.g., “median survival was 10 months in the treated vs 7 months in control.”
If you had more than two groups (say treatment A, treatment B, control), the log-rank can compare all three (giving a single p-value).
If significant, you might then do pairwise log-rank tests between each pair of groups, perhaps with a Bonferroni correction for the 3 comparisons.
Note: If some mice were still alive at 12 months, their data is censored – the log-rank properly handles that. Whereas an ordinary test on mean survival would not. Thus, always use log-rank (or Cox model) for time-to-event data. In Prism’s output, you might also see the hazard ratio if you set it up. E.g., HR = 0.5, meaning the treatment group had half the risk of death at any given time compared to controls, with a 95% confidence interval and p-value. That adds clinical meaning to the result!
Example 4: RNA-seq Differential Expression
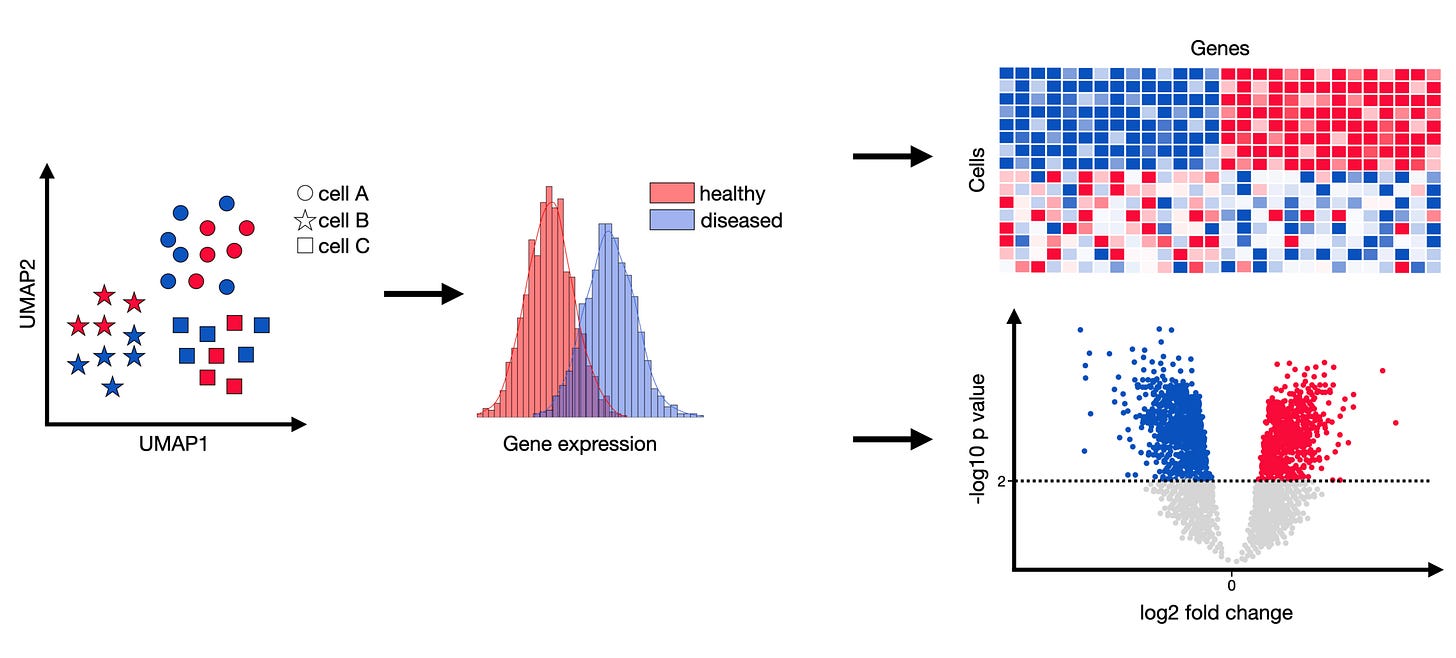
RNA-seq generates large amounts of data. (Photo credit: Single-Cell Best Practices)
Scenario
You performed RNA sequencing on cancer cells ± a drug and now have thousands of genes with expression values in each condition. Identifying which genes are significantly differentially expressed is a statistical challenge due to the sheer number of tests.
How to approach this in Prism?
Correct analysis
GraphPad Prism isn’t designed to handle thousands of genes at once with advanced models.
Full RNA-seq analysis usually requires specialized tools (DESeq2, edgeR in R).
However, let’s say you filtered down to 20 candidate genes of interest and you want to do a simple comparison of their expression between untreated vs treated (with, say, 3 biological replicates each).
You could perform multiple unpaired t-tests for those 20 genes in Prism. Instead of doing them one by one, Prism has a Multiple t tests analysis where you can input a table (genes as rows, two columns for control and treated values).
Choose “t-tests, assuming Gaussian, unpaired” and crucially select a method to correct for multiple comparisons – in this case, since you have 20 tests, using the False Discovery Rate (FDR) procedure is wise.
Prism can use the two-stage Benjamini–Krieger–Yekutieli method; you’d set say Q = 0.05 (5% FDR).
Prism will then mark which genes pass that threshold.
E.g., it might label 5 genes as significant (adjusted p < 0.05, or q<0.05). You would then report those genes as differentially expressed.
If Prism didn’t have the FDR option, a Bonferroni correction for 20 tests (which would require p<0.0025 for significance) could be too strict. FDR is more appropriate here.
Ensure you don’t just use ordinary t-test p-values for 20 genes without correction. The general principle: multiple comparisons are a huge concern in high-throughput data. Interpreting results without correction would likely yield a ton of false positives.
By using an FDR approach, you accept a controlled proportion of false hits (e.g., expect ~5% of your significant genes to be false).
If you had to use other software, you might get an adjusted p-value for each gene (Benjamini–Hochberg). The ones with adjusted p < 0.05 are your discoveries.
In a scenario where, say, TP53 mRNA is 2-fold up in treated vs control with an adjusted p = 0.001, you’d highlight that gene. In Prism, after running multiple t-tests, check the “Q” column or the significance stars that are adjusted – Prism might give each gene a “discoveries” designation.
In publication, you’d list the significantly changed genes with their fold change and adjusted p.
For RNA-seq count data specifically, t-tests are not ideal (since counts are not Gaussian). But if it’s log-transformed CPM or something, it could be passable for a small gene set.
For a comprehensive RNA-seq, use dedicated bioinformatics pipelines and then you can import top genes into Prism for plotting.
The key takeaway: always correct for multiple testing when dealing with a high number of comparisons.
VII. Software-Specific Tips for GraphPad Prism Users
If you cannot find the names of the tests we mentioned in this guide, then Prism likely changed the interface to be more user-friendly.
The analysis dialog will guide you to your correct test using natural questions like: Are your data paired? Do you assume a Gaussian distribution (parametric)?
E.g., instead of searching for “Kruskal-Wallis”, you’ll simply go to ANOVA and choose “unpaired” and “non-parametric” and run the analysis. The software will automatically switch to Kruskal-Wallis.
Here are some Prism-specific tips to help you navigate and avoid common mistakes:
Formats
When starting a new document, pick the appropriate table for your experimental design.
A “Grouped” data table is used for two-way ANOVA.
A “Column” table for simple comparisons or one-way ANOVA, and a “Survival” table for time-to-event data.
If you have repeated measures, enter data in a RM format (each subject in one row across treatments) so that Prism knows it’s paired.
If you put all values in one column with a grouping variable, Prism might treat them as ordinary one-way ANOVA (unpaired) by default. So structure your data consistent with the experiment – it prevents a lot of confusion later.
Setting up the table right will make the analysis options straightforward.
Read the Checklist
Prism often provides an analysis checklist or summary in the results.
E.g., after an unpaired t-test, it might list: “Assumed Gaussian distribution, unpaired t-test, two-tailed P value, 95% CI of difference, F test for equality of variance p=0.4 (so equal variances assumed)” etc.
Read this and add key metrics to your report. It helps ensure you did what you think you did.
If something looks off (e.g., it says “Welch corrected” when you didn’t intend that), you can go back and adjust the options.
Beware of Default Settings
Prism tries to be helpful with defaults. But you should be aware of them.
Here are some defaults:
Prism’s multiple comparisons after one-way ANOVA might use the Turkey (Tukey) test if you choose “compare all pairs” (Prism had a typo of Tukey as “Turkey” in some versions!). Make sure that’s what you want.
If you go to Multiple t tests analysis, Prism might default to no correction or to Holm-Šidák – ensure you actively select the correction method you plan (e.g., FDR for lots of tests).
For survival, Prism by default does a log-rank test; if you need a Gehan–Breslow–Wilcoxon test (which weights early differences more), you’d have to specify that.
In repeated measures ANOVA, Prism by default assumes sphericity; if violated, you should interpret with Greenhouse-Geisser correction or use the built-in mixed effects model Prism provides. The software will usually mention these in the results, but it’s on you to know what they mean.
If you’re ever confused, save this guide and go back to Section 2: “Choosing the Right Test”.
Check Graphs vs. Stats
On the left panel, Prism seamlessly links data (upper part), analyses (middle part), and graphs (lower part). If you remove an outlier from the data table, the analysis and graph update. Make sure the graph matches the stats you report.
For example:
If you log-transform data for analysis, plot the data on a log scale too or indicate that in the figure (so you figure matches the analysis)
If you run a non-parametric test, show median and quartiles on the graph instead of mean ± SD
Document… everything
One challenge with Prism (and any GUI software) is reproducibility. It’s easy to click buttons then forget exactly what you did.
As a rule, write down in your lab notebook or Methods section:
“Data were analyzed in GraphPad Prism v9.4.1. We used a one-way ANOVA followed by Tukey’s multiple comparisons test. Normality was assessed by Shapiro–Wilk test (n.s.).”
…or whatever’s appropriate.
Unlike code-based analysis, point-and-click doesn’t leave an immediate trail. So be your own audit trail.
This way, others (and future you) can understand the process.
Know Prism’s limits
Prism is great for standard tests, but it’s not omnipotent.
It doesn’t do three-way ANOVA, multivariate regression, or advanced machine learning methods.
It has no direct facility for hierarchical clustering or principal component analysis.
It can also become slow or unwieldy with large datasets.
This guide should be everything you need on Prism, but if you still find yourself fighting with Prism (e.g., tests that are not built-in, power analyses), it’s your sign to use R, Python, SPSS, or others.
Use Prism for what it’s best at: quick analyses, nice graphs, and interactive exploration of small-to-medium datasets.
Prism vs. other software
Here’s work from a fellow researcher on Reddit:
“Both [Prism and SPSS] are trustworthy, as long as you tell them to do the right thing. The limiting factor is your knowledge of statistics and how clear it is to tell the software what test to use”
Prism’s strength is making it easy to do the right thing – but it also makes it easy to do the wrong thing if you click carelessly.
Compared to R or Python, Prism won’t let you stray too far (there are only so many buttons). But code-based tools give you more flexibility (and are free).
A medical statisticians’ review commented that
“GraphPad Prism has less functionality compared to the other options, reflecting the tests and graphs its designers think their users want. It encourages a point-and-click approach, which can be very appealing for beginners, but makes it harder to update or expand analyses later”.
In other words, Prism is superb for routine analysis and visualization—just be mindful that any complex or customized analysis might require exporting data to a more powerful environment.
Exporting and Reporting
Prism allows you to directly copy results tables and even the analysis descriptions. You can paste those into a Word or Excel file as a record.
When preparing figures for publication, you can embed significance asterisks on graphs (Prism has a way to add “*p<0.05” symbols on bar graphs, etc., either automatically or manually).
Just ensure that any significance markers match the test you actually did (e.g., if you did Tukey, don’t label a comparison between two groups if that wasn’t significant in Tukey’s test, even if a simple t-test might show it – trust the post hoc).
It’s usually good practice to include the statistical test used in the figure legend for clarity.
In short,
Treat GraphPad Prism as a helpful assistant: it will do the heavy lifting of calculations and graphing, but you need to choose the right test and options.
Don’t just click through analyses without understanding them. If something isn’t clear (say, “What is the Brown-Forsythe test that Prism reported?”), check Prism’s help guide or ask on forums. The investment of a few minutes to confirm details can save you from reporting an incorrect result.
Save this guide and come back to it later. If your colleagues struggle too, share this guide with them.
VIII. Finally,
Remember that context matters.
Statistical significance is not the same as biological significance.
Always interpret your Prism results in light of the biology. A p-value tells you if an effect is likely real (not due to chance in your sample).
But you as the scientist must decide if that effect is meaningful in the bigger picture.
By choosing appropriate tests and avoiding common errors, you ensure your math supports your scientific conclusions.
Happy analyzing!